Introducción
La primera experiencia literaria para el niño es la escucha de cuentos, un momento donde puede trasladarse a otro lugar, transformarse en personajes diferentes o crear nuevos horizontes para la imaginación y la creatividad. Todos recordamos algún cuento infantil que nos evoca un recuerdo agradable, pero pocas veces tuvimos la experiencia de vivenciar una de estas historias vinculada a un contenido curricular relacionado con disciplinas científicas, como las matemáticas.
El cuento infantil es un mediador didáctico fundamental en el aprendizaje de los niños, que facilita la transmisión de mensajes simbólicos de una manera lúdica y entretenida, al tiempo que estimula su curiosidad e imaginación, elementos que podemos considerar fundamentales para el aprendizaje de los contenidos relacionados con las disciplinas científicas a través de la indagación (Bevins y Price, 2016).
La investigación que utiliza los cuentos como herramienta de aprendizaje es abundante, y nos facilita recorrer distintos objetivos de aprendizaje sobre todo en edades tempranas. El cuento proporciona distintos elementos para trabajar en el aula de infantil que van desde el desarrollo del lenguaje al trabajo con imágenes, pasando por un amplio abanico de posibilidades que se contemplan dentro de las áreas que conforman el currículo oficial (Decreto 17, 2008).
Algunos de estos abordajes concretos en las etapas iniciales de la escuela pueden ser la producción de historias con una narrativa estructurada, tras una intervención basada en la lectura y reconstrucción de cuentos (Borzone, 2005), o el conocimiento de fenómenos científicos a partir de las representaciones (Kalogiannakis et al., 2017) o aspectos centrados en emociones sociales y sentimientos, facilitando un escenario donde sea sencillo nombrarlas y reconocerlas (Sánchez et al., 2018). El cuento puede ser una herramienta para “ayudar a generar y desarrollar las conductas necesarias para incrementar la participación y la expresión emocional, tanto en situaciones de la vida normal, como en las de conflicto o crisis” (Correa, 2002, p. 140).
Desde la perspectiva de la educación matemática temprana, la investigación en didáctica de las matemáticas ha tomado relevancia en las dos últimas décadas, dando solidez a una formación de contenidos adaptada a las características personales de los niños en esta etapa educativa, prestando atención especial a los recursos que se utilizan en el aula, y aportando evidencias que muestran que las habilidades matemáticas tempranas forman la base de los aprendizajes posteriores (Claessens y Engel, 2013). El nivel de desarrollo de las competencias matemáticas tempranas se relaciona positivamente con competencias verbales, espaciales y habilidades de memoria (Locuniak y Jordan, 2008; Mazzoco y Thompson, 2005).
La instrucción matemática en los primeros años debe ser motivadora, para hacer que los niños participen desde la resolución de problemas (National Association for the Education of Young Children [NAEYC]) & National Council of Teachers of Mathematics NCTM], 2002). La enseñanza en estas etapas debe facilitar el aprendizaje de los contenidos matemáticos, al tiempo que se avive un enfoque positivo hacia su aprendizaje (Ginsburg y Golbeck, 2004), desde la creación de un entorno matemático adecuado que le lleve a conseguir experiencias a través de la manipulación (Dienes, 1990). El diseño de situaciones de aula que despierten la curiosidad da lugar al desarrollo de la capacidad de ser creativo (Casey, 2011); el maestro a través de la forma en que implementa las actividades presenta situaciones que promueven la capacidad de análisis y razonamiento de los niños facilitando su participación activa (Jacobi-Vessels et al., 2016).
No podemos olvidar la necesidad de una competencia adecuada en comunicación lingüística en el aprendizaje de las matemáticas, situación en la que trabajar con los cuentos puede contribuir desde la lectura comprensiva y la expresión correcta de los resultados obtenidos. En estas edades es importante el uso de actividades donde se vinculen las distintas áreas de contenido con la lengua natural, de forma que los niños puedan ampliar el lenguaje oral desde la escucha y la interacción con los otros. Además
el cuento encaja en perfecta sintonía con su juego simbólico, puede representarlo haciendo una imitación diferida del mismo, le permite fomentar su capacidad de abstracción entendiendo valores como «maldad, bondad, avaricia, generosidad, etc.», vivenciar sus sentimientos ante el relato manifestando sus simpatías y antipatías ante los personajes (Marín, 1999, p. 29).
La lectura de cuentos puede facilitar a los niños conocer palabras en un contexto de instrucción del sentido numérico (Hassinger-Das et al., 2015). El uso de los cuentos como herramienta para el aprendizaje de las matemáticas muestra distintos logros en la investigación didáctica. Whitin y Whitin (2004) señalan los libros de cuentos como un buen recurso para conectar los contenidos matemáticos con las situaciones reales. La lectura de relatos puede facilitar momentos donde se trabaje la lógica y la resolución de problemas (Saá, 2002). El escenario que provee un cuento nos permite trabajar con objetos con los que el niño puede interactuar, adquiriendo así capacidades lógico-matemáticas (Alsina, 2012).
Los niños construyen conocimiento matemático con actitudes positivas al utilizar los cuentos como un medio para imaginar escenarios, donde los personajes resuelven problemas (Keat y Wilburne, 2009). La creación de conexiones entre distintas situaciones es lo que da lugar a un significado de las ideas matemáticas, dando lugar en los niños a un inicio en la construcción de generalizaciones a partir de la observación (Haylock y Cockburn, 2013).
Barrera (2015) presenta una posibilidad de trabajar distintos contenidos matemáticos de una manera contextualizada en situaciones reales (conteo, operaciones, entre otros) construyendo un libro de cuentos, que puede utilizarse a partir del tercer curso de educación primaria. Colomer y Ramos (2002) diseñaron una investigación utilizando cuentos populares para trabajar los contenidos matemáticos de manera temprana, mientras que Aymerich (2010) presentó una revisión de qué cuentos pueden ser útiles para trabajar contenidos matemáticos. De manera más particular para el aprendizaje de un contenido concreto, Rodríguez y Fernández (2016) construyen un cuento para trabajar la descomposición decimal del número. El uso de la lectura en un contexto específico de una materia escolar plantea como dificultad su instrumentalización (Cerrillo, 2007), hecho que es necesario prevenir desde el diseño de la intervención educativa, teniendo como objetivo la creación de realidades y contextos no alejados de la esencia de la lectura elegida.
Por último, queremos hacer una mención a un asunto que se recoge en la investigación didáctica en relación a dos covariables, sexo y edad, bajo la hipótesis de que pueden influir en el aprendizaje de la matemática temprana. La invarianza por sexo en el aprendizaje de las matemáticas está ampliamente explorada en niveles superiores, sin embargo, los estudios en Educación Infantil (EI) no son tan frecuentes (Aragón et al., 2013; Arens et al., 2016; Navarro et al., 2010). Las posibles diferencias o similitudes de rendimiento de acuerdo al sexo, pueden considerarse desde tres focos, las habilidades aritméticas y espaciales (Bakker et al., 2019; Nowell y Hedges, 1998; Reilly et al., 2017), las estrategias de resolución de problemas (Laski et al., 2013) o la influencia del medio social y cultural (Makosz et al., 2019; Nguyen y Ryan, 2008), sin embargo, consideramos que no son situaciones disjuntas sino que ambas pueden dar lugar o no a diferencias en el aprendizaje de las matemáticas por la relación intrínseca que mantienen con sus objetivos y contenidos.
Respecto a la edad, es frecuente que los niños en el aula de infantil tengan una edad cronológica distinta de la edad madurativa, por lo que en este sentido cabe pensar que los resultados de aprendizaje se verán condicionados por esta variable. La investigación señala que la edad cronológica puede tener relación con las habilidades aritméticas (Nanu et al., 2020), e incluso que “los estudiantes que son más jóvenes que el promedio para su grado tienen más probabilidades de tener un desempeño deficiente en matemáticas” (Rodríguez, 2016, p. 5).
Así pues, situamos el cuento como una herramienta didáctica en edades tempranas, que facilita el diseño de un escenario didáctico motivador permitiendo un trabajo holístico para el logro de los objetivos de enseñanza-aprendizaje.
Objetivo
En las primeras etapas de la escolarización, un reto constante debe ser encontrar elementos que motiven a los niños por el aprendizaje, al tiempo que den lugar a situaciones donde se dé solidez a los contenidos matemáticos. Por ello, hemos querido conjugar dos focos de interés, presentados en los antecedentes: la lectura del cuento y el aprendizaje lógico-matemático. El objetivo principal es mostrar la utilidad del uso del cuento en el aprendizaje temprano de las matemáticas, desde el desarrollo de actividades a partir de su lectura; para ello nos planteamos como objetivos específicos en este trabajo: (1) adaptar el cuento del Patito Feo, configurando un escenario para el desarrollo del pensamiento lógico-matemático desde las escenas del cuento; (2) determinar si hay aspectos de logro de la competencia matemática que se diferencian entre los niños que aprendieron utilizando los cuentos y los que no, y (3) analizar las posibles diferencias por sexo y edad en el aprendizaje temprano de las matemáticas.
Método
Dadas las características de la investigación, se definió un diseño cuasiexperimental transversal de enfoque cuantitativo, con grupo control.
Participantes
La muestra de estudiantes de EI (n=62) pertenece a dos centros de titularidad concertada, situados en el centro de Madrid. La edad media en todos los grupos al inicio de la intervención es de 5 años y 9 meses.
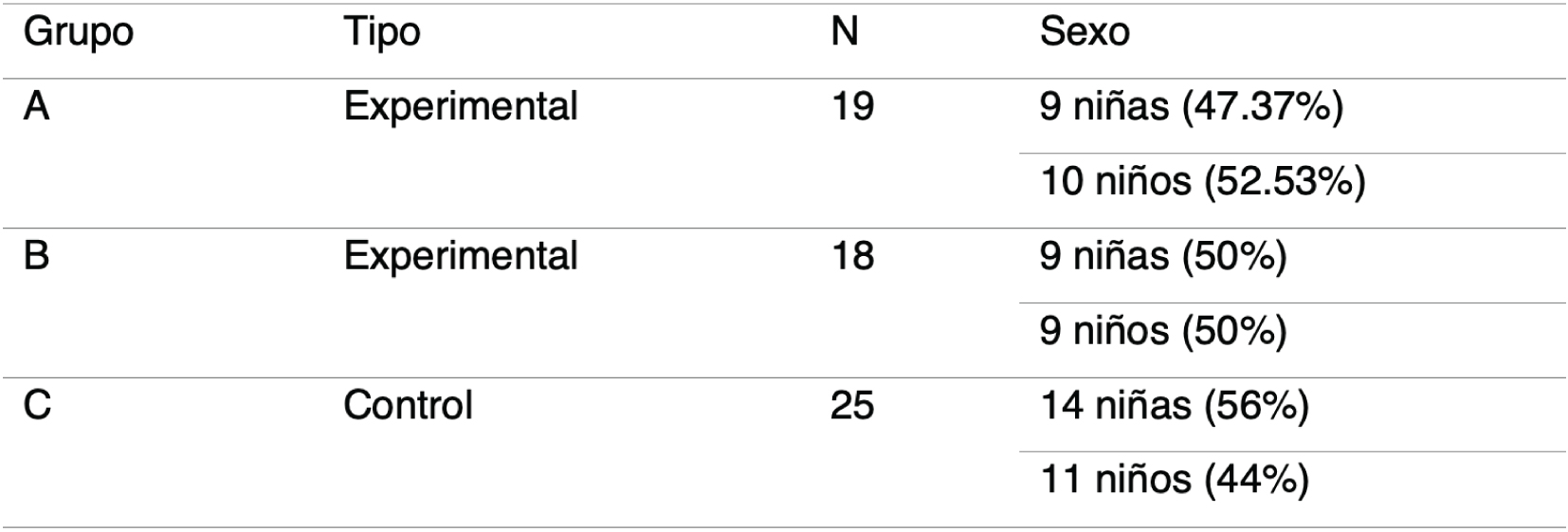
Los grupos experimental y de control se eligieron de manera aleatoria (tabla 1), pero los grupos estaban formados de manera previa.
Tabla 1
Distribución de estudiantes en los grupos control y experimental
Instrumento
Para establecer una homogeneidad en el nivel de conocimiento matemático en los grupos, se diseñó una evaluación inicial con una prueba ad hoc administrada de manera individual, formada por 9 preguntas sobre los distintos contenidos lógico-matemáticos que se recogen en el currículo de la etapa: comparación (V1), clasificación (V2), correspondencia (V3), seriación (V4), conteo verbal (V5), conteo estructurado (V6, V7), conteo resultante (V8) y conocimiento del número (V9).
Los resultados tras la intervención se midieron con la versión española del Test de Evaluación Matemática Temprana (TEMT) (Navarro et al., 2011). Consiste en una prueba individual, destinada a evaluar el nivel de competencia matemática en niños entre 4 y 7 años. La prueba tiene tres versiones (A, B y C), de 40 ítems cada una de ellas, agrupadas en 8 subtest (cuatro de habilidades lógicas, P1 a P20; y cuatro de habilidades numéricas, P21 a P40) de 5 ítems cada uno. Para esta intervención se utilizó la misma versión (A) para todos los niños. La consistencia interna del TEMT es alta (α = .95) tanto en el total de la escala como en las dos subescalas lógica (α = .94) y numérica (α = .93). La aplicación se hizo por parte de un único investigador, entrenado en el uso de este instrumento, y el tiempo de aplicación fue entre 20 y 30 minutos para cada estudiante.
El instrumento facilita la construcción de una puntuación directa, definida como nivel de competencia matemática (NCM), asignando a cada ítem un valor de 1, y obteniendo así cinco niveles A, B, C, D y E, que se etiquetan como “muy bueno, bueno, moderado, bajo y muy bajo” para cada estudiante, calculado en relación a la puntuación obtenida por su grupo.
La muestra se sitúa en el grupo de edad III del manual del TEMT (Navarro et al., 2011).
Procedimiento
El diseño del procedimiento se lleva a cabo de manera conjunta con el equipo docente de ambos colegios. Esto facilita a los investigadores centrarse en el dominio específico e identificar las necesidades reales en el aula (Cai et al., 2016).
Para este diseño se han considerado los principios metodológicos de la etapa de EI partiendo del nivel de desarrollo del alumno, el principio de actividad y el protagonismo del alumno, con aprendizajes con sentido en un entorno globalizado.
El primer paso fue un diagnóstico en las dos aulas que nos facilitó conocer las destrezas de contenidos matemáticos que tenía cada uno de los niños. La intención en este sentido era detectar posibles dificultades y asegurar un punto de partida homogéneo en ambos grupos.
El segundo paso fue el diseño de las situaciones didácticas (Brousseau, 1998) adaptadas a la realidad de los estudiantes con los que íbamos a trabajar. El cuento seleccionado fue el Patito Feo (Andersen, 1843). Consideramos que el uso de un cuento popular era una opción óptima por sus características estructurales y porque los niños conocían la historia de manera previa.
Desde el análisis de la historia original del cuento, se analizaron qué escenas (tabla 2) podrían servir para el trabajo con contenidos matemáticos en esta etapa, para elaborar actividades bien planificadas donde estos no estuviesen aislados (Cascallana, 1988). Uno de los elementos fundamentales en un cuento son las funciones de los personajes (Propp, 1981), y en este caso van a delimitar el diseño de cada actividad a partir de la acción que emprenden. El cuento del Patito Feo tiene un protagonista principal, que actúa de acuerdo a una búsqueda. El héroe se aleja de lo familiar, para tener distintas aventuras que nos centrarán en la actividad matemática, para retornar después a su lugar con nuevos aprendizajes. Esta estructura trifásica del cuento (Campbell, 1984) hace de este cuento un espacio ideal para el planteamiento de actividades de naturaleza individual y colectiva, sin necesidad de una adaptación del ciclo de la historia.
Tabla 2
Escenas del cuento y contenidos matemáticos que se trabajaron

Durante la lectura del cuento, además se trabajaron otros contenidos de manera verbal durante la asamblea. Algunos ejemplos de texto que se utilizaron de manera específica, para diseñar actividades que requiriesen movimiento por el aula (tabla 3). La integración del movimiento en el aprendizaje de las matemáticas tiene un efecto positivo en el disfrute y compromiso de los estudiantes (Riley et al., 2017). Esto son contenidos que los niños conocen ya de manera previa, y que se busca un refuerzo y consolidación de los mismos.
Tabla 3
Texto del cuento y contenido matemático desarrollado en grupo

En tercer lugar, se diseñó la estructura de la implementación en las sesiones alternando el trabajo individual y en grupo. Este trabajo se realizó de manera conjunta con la construcción de materiales. El objetivo era el uso de materiales no específicos de la didáctica, sino elaborados para la ocasión a partir de objetos de la cotidianeidad del niño. La premisa que orientó la elección fue tener “un material con el que poder realizar actividades en las que el alumno sea un agente activo y participativo de su proceso de enseñanza-aprendizaje” (Rodríguez y Fernández, 2016, p. 72).
Respecto a la puesta en escena se tuvieron en cuenta dos consideraciones: en primer lugar, que las propuestas debían adaptarse a las dinámicas realizadas por el profesor durante la jornada escolar y en segundo lugar esta planificación debía ser flexible, para adaptarse a las necesidades de los niños.
La primera de las fases en el aula es la narración oral del cuento por la maestra o el maestro. Los niños colocados en asamblea escuchan el relato mientras se les muestran las ilustraciones, bien sobre el libro en papel o de manera digital. El uso de ilustraciones capta la atención, además de facilitar la comprensión y memoria en los niños (Follmer y Semb, 2008). Cuando los niños intervienen o hacen preguntas, la lectura se detiene para atenderles, estos interrogantes “son de una gran riqueza a la hora de emplear el cuento como herramienta de aprendizaje, ya que nos permiten seguir el hilo de la comprensión y adquisición por los niños de los contenidos que aparecen en el relato” (Marín, 2013, p. 9). La forma de incorporar estas preguntas a la narración será la tarea más importante del docente, porque hará que el aprendiz alimente y acreciente su curiosidad porque “el cuento no es solamente para entretener, sino para causar y ser causa de revoluciones. No se narra únicamente para saber más, se narra para aprender a preguntar y para generar más y mejores preguntas” (Agudelo, 2016, p.14).
Una vez el maestro ha finalizado el relato se inicia de nuevo la narración, pero esta vez cada escena viene reforzada por el uso de los distintos materiales de uso didáctico. El objetivo es hacer perceptibles los contenidos matemáticos que se quieren trabajar; esta fase es la que se repite cada jornada de trabajo atendiendo a cada una de las actividades.
Resultados
Los resultados del diagnóstico inicial evidencian que no hay diferencias entre el grupo control y el experimental en ninguno de los ítems, por lo que se puede considerar un diseño de grupo control equivalente. La tabla 4 muestra los p-valores correspondientes al contraste de Chi-cuadrado, donde la hipótesis nula establece que no hay diferencias en las respuestas (porcentaje de aciertos) entre los grupos control y experimental.
Tabla 4
Resultados diagnóstico inicial

Nota:a=variable constante; aciertan todos en los dos grupos
Además, podemos señalar que el nivel de desempeño de éxito en cada uno de ellos se encuentra siempre por encima del 50%, tal como puede apreciarse en la figura 1.
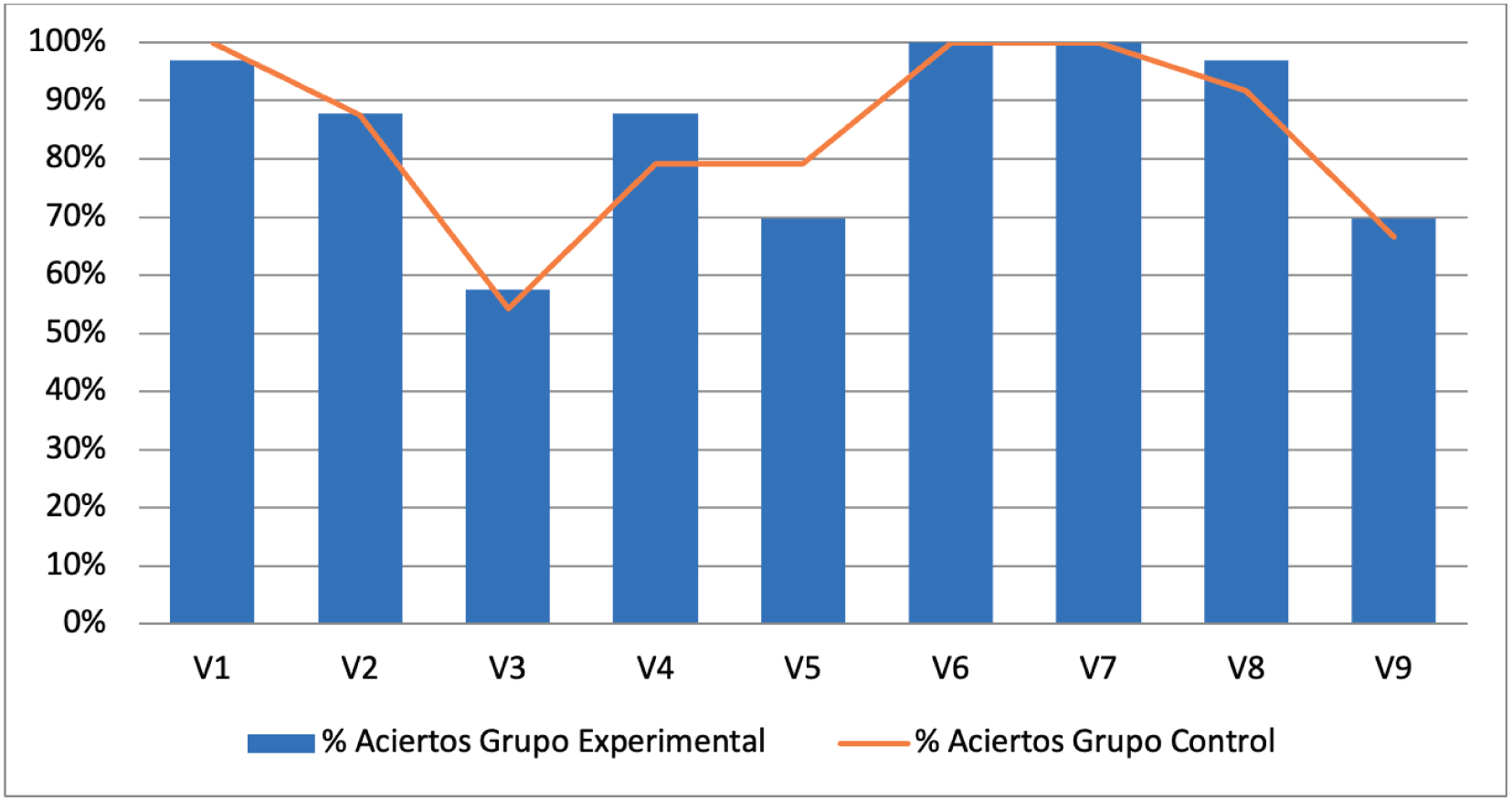 Figura 1
Resultados del diagnóstico inicial
Figura 1
Resultados del diagnóstico inicial
En cuanto a los resultados tras la intervención, los porcentajes de acierto en los grupos experimental y control en cada uno de los bloques de habilidades (figuras 2 y 3), señalan mejores resultados en casi todos los ítems para el grupo experimental.
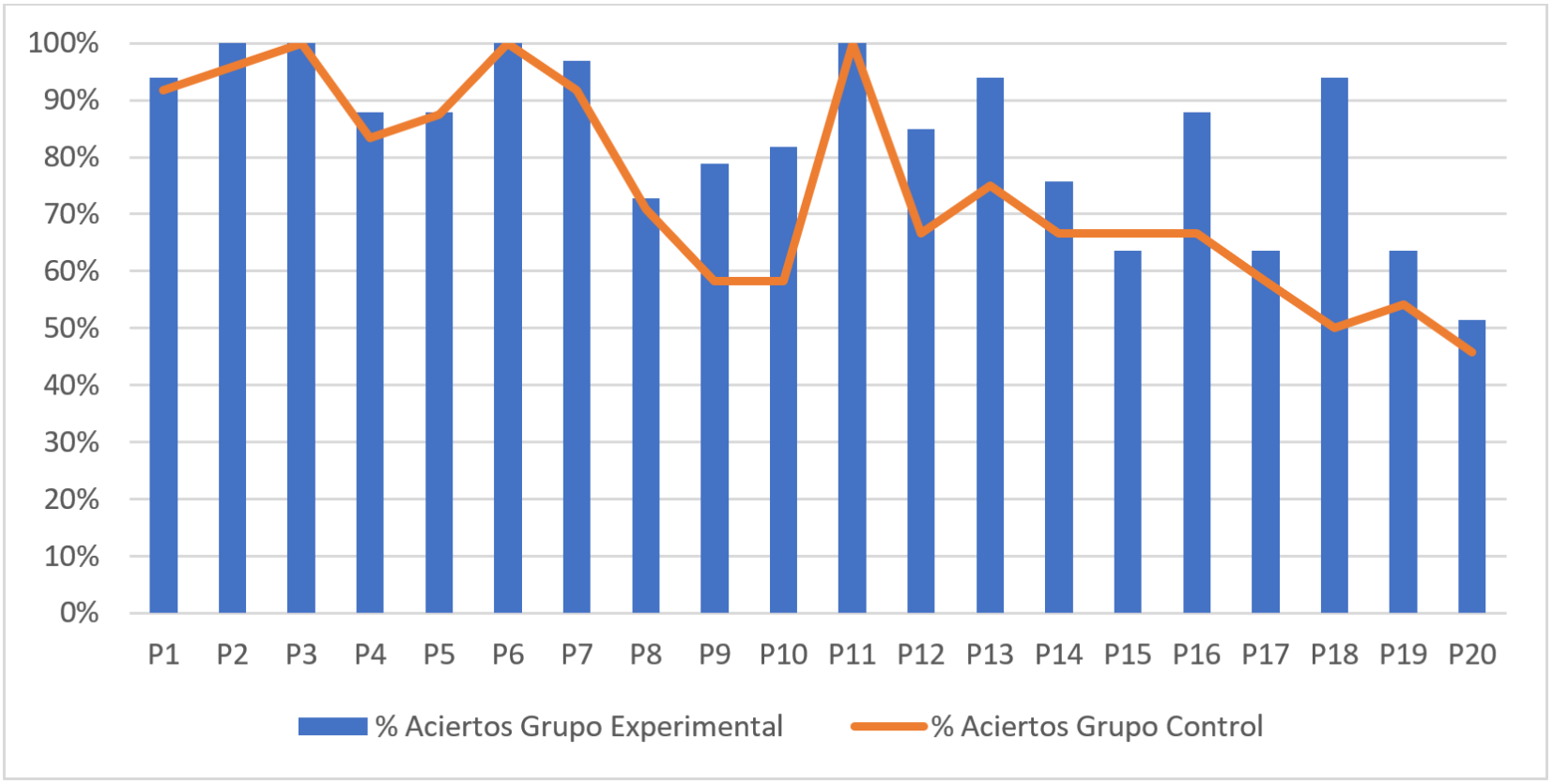 Figura 2
Resultados TEMT para habilidades lógicas
Figura 2
Resultados TEMT para habilidades lógicas
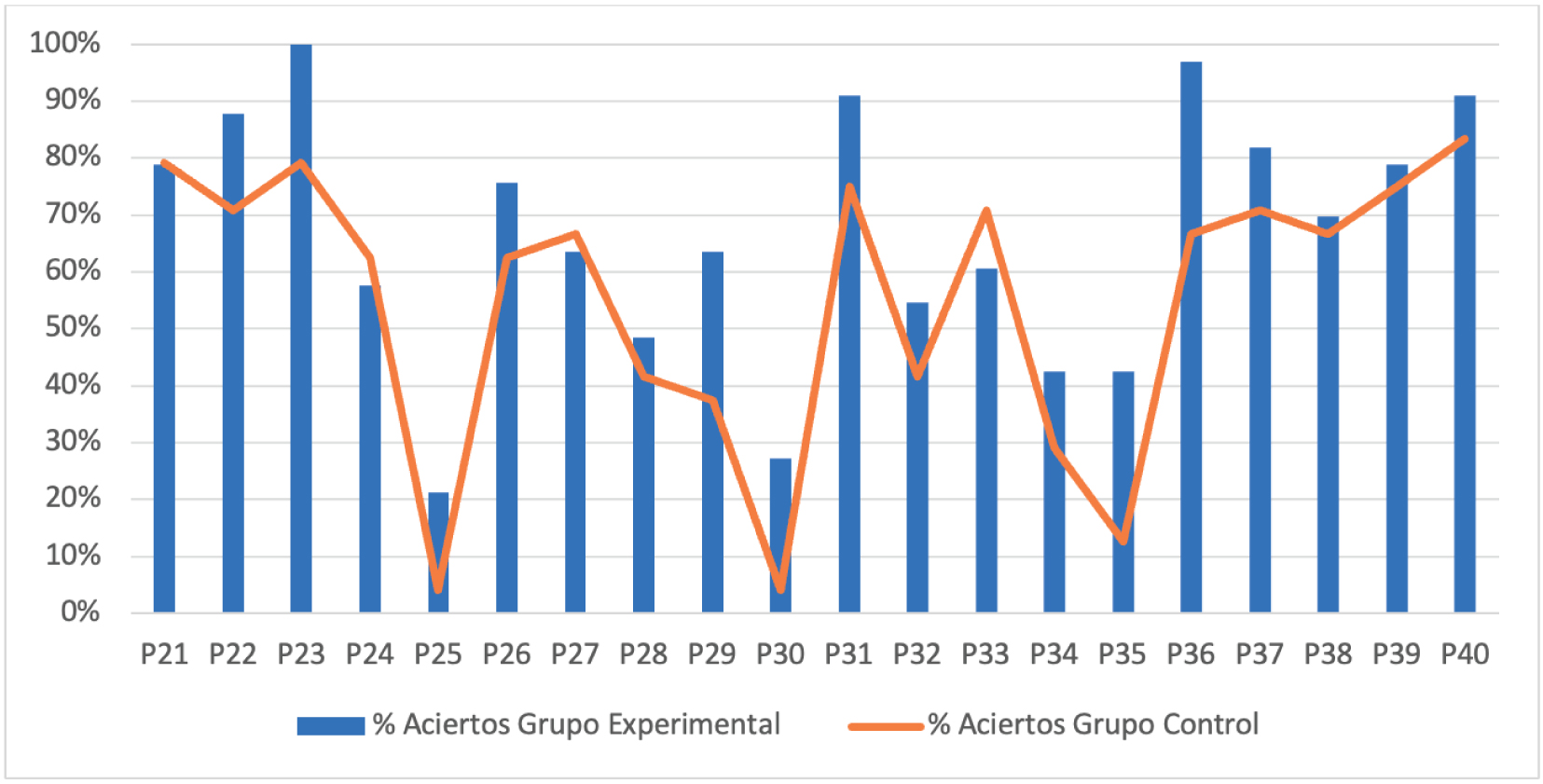 Figura 3
Resultados TEMT para habilidades numéricas
Figura 3
Resultados TEMT para habilidades numéricas
Los ítems con resultados inferiores en el grupo experimental son P15, P24, P27 y P33, pese a estas diferencias encontradas a favor del grupo control ninguna de ellas resulta estadísticamente significativa. La tabla 5 recoge aquellos ítems que sí muestran estas diferencias a favor del grupo experimental.
Cabe mencionar cuatro ítems que muestran resultados bajos en ambos grupos, P25, P30, P34 y P35, todos ellos relacionados con habilidades de conteo. Estos ítems coinciden con los únicos que se consideran “muy difíciles” en el manual de TEMT, con un índice de dificultad por debajo de .25.
En P25 se solicita contar de dos en dos hasta 14; P30 tiene como objetivo a la vista de objetos el conteo hacia atrás desde 17; P34 recoge cómo los niños cuentan 19 objetos sin posibilidad de manipularlos, mientras que P35 tiene como objetivo que los niños cuenten hasta 12 pero como parte de una estrategia aditiva, dando primero 5 objetos que se ocultan y añadiendo más tarde 7 más.
Tabla 5
Resultados de los ítems del instrumento TEMT que resultan estadísticamente significativos
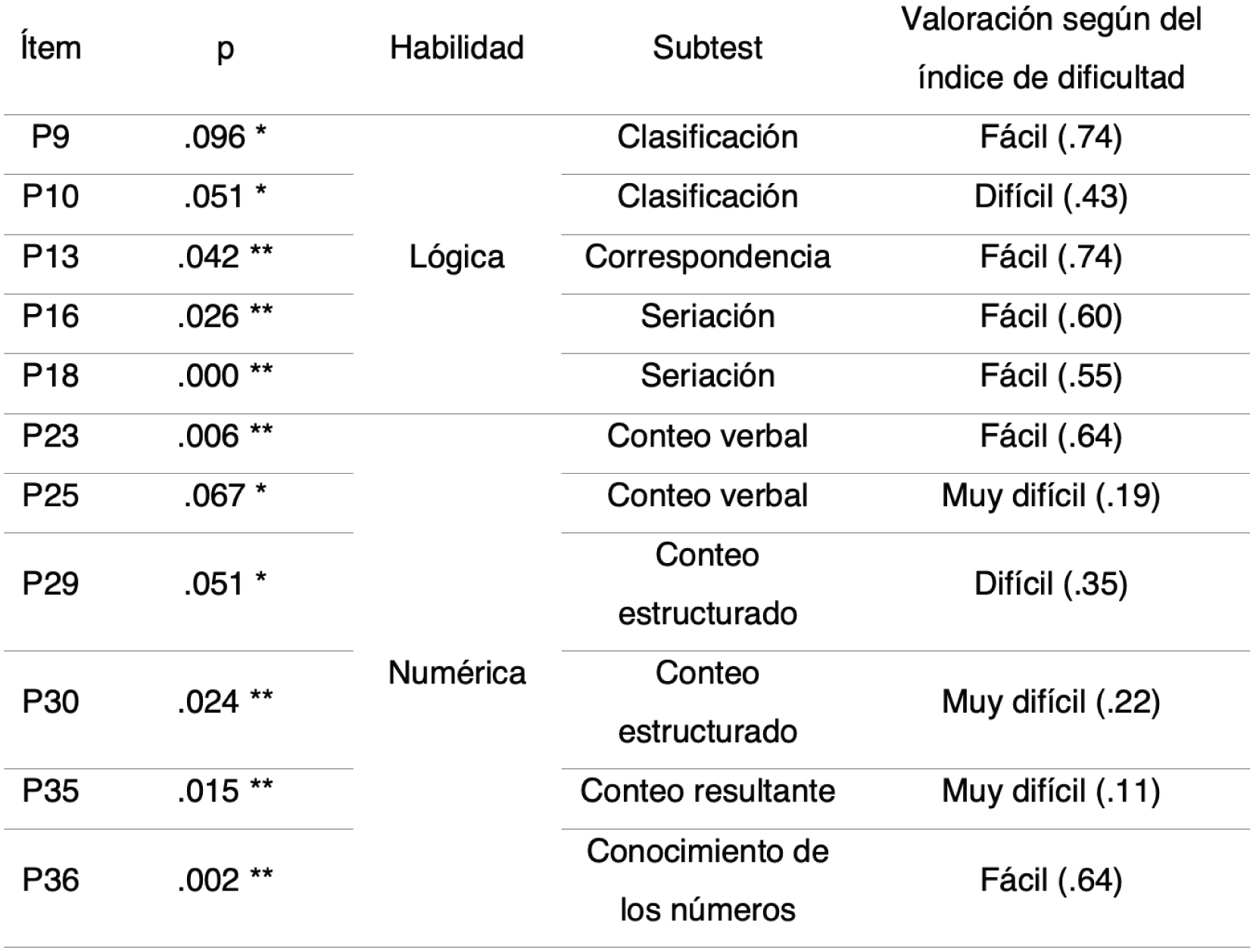
Nota: *=p<.05
**=p<.10
Como podemos observar las diferencias significativas, que siempre indican mejores resultados en el grupo experimental, se muestran de manera ligeramente superior en el bloque correspondiente al trabajo numérico, con seis ítems, frente a los cinco del bloque lógico.
Estas diferencias se producen en 3 de los 4 ítems considerados de mayor dificultad en el instrumento.
Los ítems P15 y P24 (figura 4) focalizan su atención en instrucciones donde la representación utilizada para los objetos es demasiado compacta. En P15 se busca que el niño cuente el número de globos y señale cuál de los cuadros inferiores tiene el mismo número de puntos (conteo), y en P24 se pide al niño que localice la flor número 18 (ordinal).
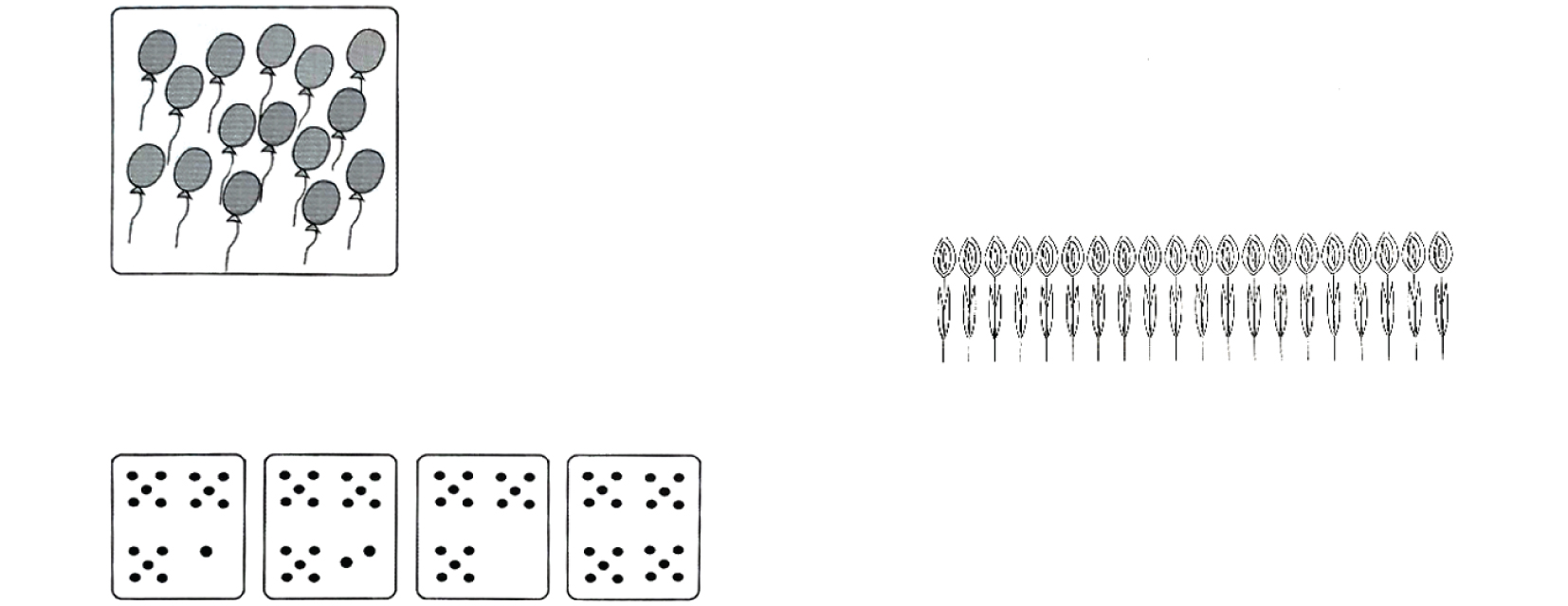 Figura 4
Ficha de evaluación de los ítems 15 y 24 del TEMT, modelo A.
Figura 4
Ficha de evaluación de los ítems 15 y 24 del TEMT, modelo A.
Estos resultados se confirman cuando calculamos el NCM para cada uno de los estudiantes de ambos grupos, y se contrastan con un test t de Student, previa comprobación del supuesto de normalidad en los dos grupos (pruebas de Kolmogorov-Smirnov con la corrección de Lilliefors y Shapiro-Wilk), obteniéndose diferencias significativas con mejores resultados globales en el grupo experimental. En concreto, la media toma un valor de 30.5 en el grupo experimental y de 25.9 en el de control, rechazándose la hipótesis nula de igualdad de medias (p = .002).
Respecto a las diferencias por sexo, el contraste de Chi-cuadrado refleja que son pocos los ítems con resultados diferenciales (tabla 6). En todos ellos los resultados son mejores en las chicas.
Tabla 6
Resultados de los ítems del instrumento TEMT que indican diferencias por sexo

Nota: *=p<.05
**=p<.10
Destacan de manera particular los ítems P9 y P24 por la tipología de objeto que buscan identificar, un bolso en el ítem P9 (figura 5) y flores en el ítem P24.
 Figura 5
Ficha de evaluación del ítem 9 del TEMT, modelo A.
Figura 5
Ficha de evaluación del ítem 9 del TEMT, modelo A.
Respecto al posible impacto de la edad, medida en días, puede afirmarse que esta variable no es significativa en el análisis. Para comprobarlo, se han ajustado regresiones logísticas donde se ha introducido la edad como variable independiente. En ningún caso se ha encontrado significatividad al 5% y en los pocos casos donde había significatividad al 10% (tabla 7) el impacto era prácticamente nulo (coeficiente beta de la regresión logística muy cercano a 0).
Tabla 7
Resultados de los ítems del instrumento TEMT que indican diferencias por edad

De nuevo hemos comprobado si aparecen diferencias en relación al sexo y edad utilizando el valor del NCM de cada uno de los estudiantes para los dos grupos, y no se han obtenido diferencias significativas en relación a ninguna de las dos variables. No existe evidencia estadística significativa para rechazar normalidad e igualdad de medias (p=.740), e incorrelación entre NCM y edad (p=.277).
De manera complementaria a la información aportada por el instrumento, en las reuniones diarias entre el equipo docente e investigador se pudieron valorar otros resultados cualitativos de la experiencia -fruto de la observación en el aula- como la rápida y espontánea adquisición de la expresión lingüística de los contenidos matemáticos en los niños.
Discusión y conclusiones
El objetivo específico inicial fue desarrollar la adaptación de un cuento a un escenario específico para el desarrollo del pensamiento lógico-matemático. Los resultados expuestos de manera previa desde las diferentes escenas del cuento muestran este contexto como facilitador para el aprendizaje temprano de los contenidos matemáticos. La formación matemática puede mejorar si el aprendizaje se sitúa en un contexto que facilite las interacciones sociales, donde los niños puedan construir conocimiento a partir de las experiencias vividas (Sawatzki y Sullivan, 2018). Este contexto puede ser construido a partir de la historia que el cuento relata, como una conexión con el entorno del niño que le motive para aprender desde la curiosidad y el interés, facilitando la visualización de conceptos matemáticos desde acciones concretas a contenidos más abstractos (Maričić et al., 2017).
Una de las ventajas de combinar las matemáticas y la literatura en el aula de EI es que ambas áreas de contenidos no están desconectadas, y que podemos considerar este tipo de intervenciones como un medio “para construir comprensión y entusiasmo y una forma de descubrir conceptos matemáticos” (Kribs y Ruebel, 2008, p. 36). El hecho de mantener niveles altos de motivación a la lectura, puede ser beneficioso desde la relación recíproca existente con la habilidad lectora (Hebbecker et al., 2019).
El segundo objetivo específico centrado en determinar la influencia de la experiencia didáctica en el logro de la competencia matemática muestra resultados más favorables en los estudiantes que participaron en la intervención con el cuento. Estos resultados destacan especialmente en las distintas estrategias de conteo. Estos principios de conteo facilitan las posibilidades posteriores de cálculos aritméticos sin la necesidad de contar (Jordan y Dyson, 2013). Se observan mejores resultados en un 27.5% de los ítems del instrumento en el grupo experimental, mientras que el resto tienen los mismos resultados.
En los cuatro subtest de habilidades lógicas podemos señalar mejoras en clasificación y seriación fundamentalmente, esto concuerda con la tipología de actividades presentadas sobre todo las realizadas en formato individual. En cuanto a los resultados en las habilidades numéricas, destacan los resultados en conteo verbal fundamentalmente en la secuencia de palabras numéricas, tanto de uno en uno como de dos en dos.
Destacamos además en este bloque que los ítems considerados de mayor dificultad en el instrumento para este grupo de edad muestran diferencias significativas a favor del grupo experimental en tres de ellos (P25, P30 y P35). Los resultados en los ítems P25 y P30 centrados en los dos últimos niveles adquisición de la secuencia numérica, nivel de cadena numerable y nivel de cadena bidireccional, se pueden justificar desde el trabajo de sistematización de la secuencia numérica desde el contexto ordinal (Fernández, 2016).
En los ítems de conocimiento general de los números, que se muestran desde un problema verbal, encontramos mejoras en uno de los ítems del bloque (P36), un aspecto que se ha trabajado desde la recreación de situaciones problema en actividades grupales con el cuento.
Los resultados comparativos de la puntuación global del instrumento como nivel de competencia matemática señalan mejores resultados en el grupo experimental.
En relación al objetivo que planteaba un análisis de los aprendizajes matemáticos, utilizando como variables diferenciales el sexo y la edad, podemos decir que se han observado escasas diferencias, coincidiendo con investigaciones previas (Alsina y Berciano, 2018; Navarro et al., 2010).
Aunque la investigación ha alcanzado sus objetivos específicos y por lo tanto el general demostrando la utilidad del uso del cuento en el aprendizaje temprano de las matemáticas, es necesaria una reflexión para futuras investigaciones, dado que se ha realizado con una pequeña muestra. Además, conviene realizarla en un periodo de intervención más largo y con más de un cuento para comprobar los efectos de la historia, e incluso de la tipología de materiales utilizados o el uso de cuentos construidos de manera específica para el aprendizaje de las matemáticas. Asimismo, consideramos conveniente revisar el instrumento que se ha utilizado, dado que algunos resultados se condicionan por la tipología de las ilustraciones en los objetos a contar. El instrumento futuro debe recoger además en este tipo de intervenciones la evaluación de los contenidos relacionados con la geometría, en la misma línea de las recomendaciones dadas en investigaciones recientes (Assel et al., 2020), sustentadas en la consideración de esta como base para el desarrollo de razonamientos más abstractos (Geary, 2007).
Referencias
Alsina, A. (2012). Cómo desarrollar el pensamiento matemático de 0 a 6 años. Octaedro.
Alsina, A., & Berciano, A. (2018). Developing informal mathematics in early childhood education. Early Child Development and Care, 1-19. https://doi.org/10.1080/03004430.2018.1555823
Andersen, H. C. (1843). Den grimme ælling [El Patito Feo]. Nye eventyr. Første Bind. Første Samling.
Arens, A. K., Marsh, H. W., Craven, R. G., Yeung, A. S., Randhawa, E., & Hasselhorn, M. (2016). Math self-concept in preschool children: Structure, achievement relations, and generalizability across gender. Early Childhood Research Quarterly, 36, 391-403. https://doi.org/10.1016/j.ecresq.2015.12.024
Aragón, E. L., Delgado, C. I., Aguilar, M., Araújo, A., & Navarro, J. I. (2015). Estudio de la influencia de la inteligencia y el género en la evaluación matemática temprana. European journal of education and psychology, 6(1). https://doi.org/10.30552/ejep.v6i1.90
Assel, M. A., Montroy, J. J., Williams, J. M., Foster, M., Landry, S. H., Zucker, T., Crawford, A., Hyatt, H., & Bhavsar, V. (2020). Initial Validation of a Math Progress Monitoring Measure for Prekindergarten Students. Journal of Psychoeducational Assessment, 1-19. https://doi.org/10.1177/0734282920922078
Aymerich, C. (2010). Una mà de contes matemàtics. Biaix, 28-29, 32-36.
Bakker, M., Torbeyns, J., Wijns, N., Verschaffel, L., & De Smedt, B. (2019). Gender equality in 4-to 5-year-old preschoolers’ early numerical competencies. Developmental science, 22(1), e12718. https://doi.org/10.1111/desc.12718
Barrera, H. (2012). Cuéntamemates. Beginbook Ediciones.
Bender, A., & Beller, S. (2012). Nature and culture of finger counting: Diversity and representational effects of an embodied cognitive tool. Cognition, 124(2), 156-182. https://doi.org/10.1016/j.cognition.2012.05.005
Bevins, S., & Price, G. (2016). Reconceptualising inquiry in science education. International Journal of Science Education, 38(1), 17-29. https://doi.org/10.1080/09500693.2015.1124300
Borzone, A. M. (2005). La Lectura de Cuentos en el Jardín Infantil: Un Medio Para el Desarrollo de Estrategias Cognitivas y Lingüísticas. Psykhe (Santiago), 14(1), 192-209. https://doi.org/10.4067/S0718-22282005000100015
Brousseau G. (1998). Théorie des Situations Didactiques. La Pensée Sauvage.
Cai, H., Lin, L., & Gu, X. (2016). Using a semantic diagram to structure a collaborative problem solving process in the classroom. Educational Technology Research and Development, 64, 1207-1225. https://doi.org/10.1007/s11423-016-9445-6
Carney, R. N., & Levin, J. R. (2002). Pictorial Illustrations Still Improve Students' Learning from Text. Educational Psychology Review, 14, 5-26. https://doi.org/10.1023/A:1013176309260
Campbell, J. (1984). El héroe de las mil caras. Psicoanálisis del mito. Fondo de cultura económica.
Cascallana, M. T. (1988). Iniciación a la matemática. Materiales y recursos didácticos. Santillana.
Cerrillo, P. (2007). Literatura Infantil y Juvenil y educación literaria: Hacia una nueva enseñanza de la literatura. Octaedro.
Claessens, A., & Engel, M. (2013). How important is where you start? Early mathematics knowledge and later school success. Teachers College Record, 115, 1–29.
Clements, D. H., & Sarama, J. (2014). Learning and teaching early math: The learning trajectories approach. Routledge. https://doi.org/10.4324/9780203520574
Colomer, T., & Ramos, N. (2002). Treballem matemàtiques amb els contes populars. Biaix, 20, 20-25.
Decreto 17/2008, de 6 de marzo, del Consejo de Gobierno, por el que se desarrollan para la Comunidad de Madrid las enseñanzas de la Educación Infantil. Boletín Oficial de la Comunidad de Madrid, 73, 13-16. https://www.bocm.es/boletin/CM_Orden_BOCM/2018/03/26/BOCM-20180326-1.PDF
Fernández, C. (2016). Una propuesta didáctica para trabajar la secuencia numérica en el segundo ciclo de educación infantil. Enseñanza de las ciencias, 34(2), 185-204. https://doi.org/10.5565/rev/ensciencias.1798
Fernández, C. (2018). Pensamiento numérico: evolución del número cardinal en Educación Infantil. Educação Matemática Debate, 2(5), 188-204. https://doi.org/10.24116/emd25266136v2n52018a03
Follmer, A., & Semb, P. A. (2008). Do illustrations enhance preschoolers’ memories for stories? Age-related change in the picture facilitation effect. Journal of Experimental Child Psychology, 99(4), 271-287. https://doi.org/10.1016/j.jecp.2007.06.005
Geary, D. C. (2007). An evolutionary perspective on learning disability in mathematics. Developmental Neuropsychology, 32, 471–519. https://doi.org/10.1080/87565640701360924
Ginsburg, H. P., & Golbeck, S. L. (2004). Thoughts on the future of research on mathematics and science learning and education. Early childhood research quarterly, 19(1), 190-200. https://doi.org/10.1016/j.ecresq.2004.01.013
Hannula-Sormunen, M.M., McMullen, J., & Lehtinen E. (2019). Everyday Context and Mathematical Learning: On the Role of Spontaneous Mathematical Focusing Tendencies in the Development of Numeracy. In A. Fritz, V. Haase, & P. Räsänen (Eds.), International Handbook of Mathematical Learning Difficulties. Springer. https://doi.org/10.1007/978-3-319-97148-3_3
Hassinger-Das, B., Jordan, N. C., & Dyson, N. (2015). Reading stories to learn math: Mathematics vocabulary instruction for children with early numeracy difficulties. The Elementary School Journal, 116(2), 242–264. https://doi.org/10.1086/683986
Haylock, D., & Cockburn, A. (2013) Understanding Mathematics in the Lower Primary Years. Paul Chapman.
Hebbecker, K., Förster, N., & Souvignier, E. (2019). Reciprocal effects between reading achievement and intrinsic and extrinsic reading motivation. Scientific Studies of Reading, 23(5), 419–436. https://doi.org/10.1080/10888438.2019.15984
Hong, H. (1996). Effects of mathematics learning through children's literature on math achievement and dispositional outcomes. Early childhood research quarterly, 11(4), 477-494. https://doi.org/10.1016/S0885-2006(96)90018-6
Kalogiannakis, M., Nirgianaki, G. M., & Papadakis, S. (2018). Teaching magnetism to preschool children: The effectiveness of picture story reading. Early Childhood Education Journal, 46(5), 535-546. https://doi.org/10.1007/s10643-017-0884-4
Keat, J. B., & Wilburne, J. M. (2009). The Impact of Storybooks on Kindergarten Children's Mathematical Achievement and Approaches to Learning. Online Submission, 6(7), 61-67.
Keuch, S., & Brandt, B. (2020). ‘You Are Already Bigger Than the Giraffe!’—The Use of Adjectives in Measurement Activities in Kindergarten. In M. Carlsen, I. Erfjord & P. Hundeland (Eds.). Mathematics Education in the Early Years. Springer. https://doi.org/10.1007/978-3-030-34776-5_22
Kribs, C. M., & Ruebel, K. K. (2008). Exploring mathematical concepts in literature. Middle School Journal, 40(1), 36-42. https://doi.org/10.1080/00940771.2008.11461663
Jacobi-Vessels, J.L., Todd Brown, E., Molfese, V.J., & Do, A. (2016). Teaching Preschoolers to Count: Effective Strategies for Achieving Early Mathematics Milestones. Early Childhood Education Journal, 44, 1-9. https://doi.org/10.1007/s10643-014-0671-4
Jordan, N. C., & Dyson, N. (2013). Number Sense Interventions. Paul H. Brookes Publishing.
Laski, E., Casey, B., Yu, Q., Dulaney, A., Heyman, M., & Dearing, E. (2013). Spatial skills as a predictor of first grade girls’ use of higher level arithmetic strategies. Learning and Individual Differences, 23(1), 123-130. https://doi.org/10.1016/j.lindif.2012.08.001
Locuniak, M. N., & Jordan, N. C. (2008). Using kindergarten number sense to predict calculation fluency in second grade. Journal of learning disabilities, 41(5), 451-459. https://doi.org/10.1177/0022219408321126
Makosz, S., Zambrzycka, J., & Kotsopoulos, D. (2019). The “Girl Crisis”: The Relationship Between Early Gender Differences and Future Mathematical Learning and Participation. In K. Robinson, H. Osana & D. Kotsopoulos (Eds.), Mathematical Learning and Cognition in Early Childhood. Springer. https://doi.org/10.1007/978-3-030-12895-1_2
Maričić, S. M., Stakić, M. M., & Malinović-Jovanović, N. T. (2018). The Role of Literary Content for Children in Preschool Mathematics Education. Eurasia Journal of Mathematics, Science and Technology Education, 14(2), 631-642. https://doi.org/10.12973/ejmste/80627
Mazzocco, M. M., & Thompson, R. E. (2005). Kindergarten predictors of math learning disability. Learning Disabilities Research & Practice, 20(3), 142-155. https://doi.org/10.1111/j.1540-5826.2005.00129.x
National Association for the Education of Young Children (NAEYC), & National Council of Teachers of Mathematics (NCTM). (2002). Early childhood mathematics: Promoting good beginnings. A joint position statement. https://www.naeyc.org/sites/default/files/globally-shared/downloads/PDFs/resources/position-statements/psmath.pdf
Nanu, C., Laakkonena, E., & Hannula-Sormunen, M. (2020). The Effect of First School Years on Mathematical Skill Profiles. Frontline Learning Research, 8(1), 56-75. https://doi.org/10.14786/flr.v8i1.485
Navarro, J. I., Aguilar, M., García, M., Menacho, I., Marchena, E., & Alcalde, C. (2010). Diferencias en habilidades matemáticas tempranas en niños y niñas de 4 a 8 años. Revista española de pedagogía, 245, 85-98.
Navarro, J.I., Aguilar, M., Alcalde, C., Marchena, E., Ruiz, G., Menacho, I., & Sedeño, M. (2011). Test de Evaluación Matemática de Temprana (TEMT). Versión Española. Dpto de Psicología. EOS. Versión original: Van Luit, J., Van de Rijt, B. y Pennings, A. (1998). The Utrecht Early Mathematical Competence Test. Graviant.
Nguyen, D., & Ryan, A. (2008). Does stereotype threat affect test performance of minorities and women? A meta-analysis of experimental evidence. Journal of Applied Psychology, 93, 1314-1334. https://doi.org/10.1037/a0012702
Nowell, A., & Hedges, L.V. (1998). Trends in gender differences in academic achievement from 1960-1994: An analysis of differences in mean, variance, and extreme scores. Sex Roles, 39, 21-43. https://doi.org/10.1023/A:1018873615316
Propp, V. (1981). Morfología del cuento. Fundamentos.
Reilly, D., Neumann, D.L., & Andrews, G. (2017) Gender Differences in Spatial Ability: Implications for STEM Education and Approaches to Reducing the Gender Gap for Parents and Educators. In M. Khine (Eds.), Visual-spatial Ability in STEM Education. Springer. https://doi.org/10.1007/978-3-319-44385-0_10
Riley, N., Lubans, D., Holmes, K., Hansen, V., Gore, J., & Morgan, P. (2017). Movement-based Mathematics: Enjoyment and Engagement without Compromising Learning through the EASY Minds Program. Eurasia Journal of Mathematics, Science and Technology Education, 13(6), 1653-1673. https://doi.org/10.12973/eurasia.2017.00690a
Rodríguez, A. I. (2016). Impact of Chronological Age Differences on the Academic Performance of Students in a First-Grade Classroom. Journal of Interdisciplinary Undergraduate Research, 8, Article 2, 1-23.
Rodríguez, M. M., & Fernández, N. (2016). Dinosaurios que comen uvas y viven en cuevas. El cardinal numérico. NÚMEROS. Revista de didáctica de las matemáticas, 91, 69-90.
Saá, M. D. (2002). Las matemáticas de los cuentos y las canciones. EOS.
Sánchez, L., Benítez, R., & Aguilar, S. (2018). El triángulo de la educación infantil: los cuentos, las emociones y las TIC. Hachetetepé. Revista científica de Educación y Comunicación, 16, 29-38. https://doi.org/10.25267/Hachetetepe.2018.v1.i16.4
Sawatzki, C., & Sullivan, P. (2018) Shopping for Shoes: Teaching Students to Apply and Interpret Mathematics in the Real World. International Journal of Science and Mathematics Education, 16, 1355–1373. https://doi.org/10.1007/s10763-017-9833-3
Swoboda, E., & Vighi, P. (2016). Early geometrical thinking in the environment of patterns, mosaics and isometries. Springer Nature. https://doi.org/10.1007/978-3-319-44272-3
White, J. (2017). Using Children’s Literature to Teach Problem Solving in Math Addressing the Standards for Mathematical Practice in K–5. Routledge.
Whitin, P., & Whitin, D. (2004). New Visions for Linking Literature and Mathematics. The National Council of Teachers of English.
Notas de autor
* Correspondencia: blanca.arteaga@edu.uned.es